디지안의 개발일지
봉투 암호화 본문
봉투 암호화
Date: March 11, 2025
암호화에 대해서 전혀 배경지식이 없어서 정리하려고 한다. 고전 암호화부터 현재 많이 쓰이는 봉투 암호화 또는 하이브리드 암호화까지 왜 사용하게 되었는지를 중점으로 정리하려고 한다.
암호화란
위키백과에 따르면 암호화는 특별한 지식을 소유한 사람들을 제외하고는 누구든지 읽어볼 수 없도록 알고리즘을 이용하여 정보를 전달하는 과정이다 그리고 그 결과물이 암호문이다. 즉, 자기들끼리만 알려고 다른 사람들은 못 알아보도록 만드는 과정이다. 개념을 정리하면
- 평문(Plaintext): 원래의 데이터
- 암호화(Encryption): 평문을 특정 알고리즘과 키를 사용해 변환하는 과정
- 암호문(Ciphertext): 암호화된 결과물
- 복호화(Decryption): 암호문을 다시 평문으로 변환하는 과정
고전 암호화
초창기 암호화 방식은 매우 단순하였다. 대표적인 암호화 방식으로 시저 암호(Caesar Cipher)로 알파벳을 일정한 거리만큼 이동하여 암호화하는 방식이다.
예를 들어, 알파벳을 3칸 이동하여 표기하는 것이다.
- 평문 :
HELLO - 암호문 :
KHOOR
이런 방식은 암호화할 때 어떤 알고리즘을 사용했는지 알면 금방 복호화할 수 있다. 그렇다 매우 치명적이다. 반대로 수행하면 되니까. 그래서 현대에는 많이 사용하지 않는다.
아직도 사용되는 분야가 있다는데 OTP 같은 경우 아직도 고전 암호화방식을 채택한다고 한다. 비젠에르 암호 와 매우 유사하다고 하는데 자세히 알아보지는 않았다.
현대 암호화
고전 암호화를 보완하기 위해서 현대 암호화에서는 암호화에 대한 키를 관리한다. 복호화를 하기 위해서는 어떤 알고리즘으로 암호화를 했냐뿐만 아니라 어떤 키로 암호화했냐도 알아야 한다.
키를 통한 암호화 방식은 크게 두가지가 있다.
- 대칭키
- AES(Advanced Enrtyption Standard)
- 비대칭키
- RSA(Rivest-Shamir-Adleman)
AES
AES는 대칭키 방식 중에 한 알고리즘으로 블록 암호화 방식을 사용한다. 블록 암호화 방식은 일정한 크기(블록)로 나눠서 평문을 암호문으로 암호화하고 데이터의 크기가 블록보다 작으면 패딩을 추가하는 형식으로 구성한다.
패딩을 채우는 방식은 아래와 같은 예시가 있다.
| 패딩 방식 | 설명 |
|---|---|
| PKCS#7 | 부족한 바이트 개수만큼 값 추가 |
| ISO/IEC 7816-4 | 80로 시작하고 나머지는 00으로 채움 |
| Zero Padding | 00으로 채우는데, 평문에 00이 포함될 경우 문제가 생길 수 있음 |
블록 모드에 따라 패딩 없이 사용할 수도 있다. 예시는 아래와 같다.
| 패딩 방식 | 설명 |
|---|---|
| ECB (Electronic Codebook) 모드 | 패턴이 반복되므로 보안에 취약해서 사용하지 않음. |
| CBC (Cipher Block Chaining) 모드 | IV(초기 벡터)와 함께 사용하며, 패딩이 필요함. |
| CTR (Counter) 모드 | 스트림 방식으로 변환되어 패딩이 필요 없음. |
| GCM (Galois/Counter Mode) 모드 | 패딩 없이도 사용할 수 있고 인증 기능도 제공. |
AES를 통해 암호화 되는 과정은 아래와 같다.
- 입력(128비트 평문)
54 68 20 67 61 20 6D 69
73 73 69 73 73 69 70 70- 키(128비트 키)
2B 7E 15 16 28 AE D2 A6
AB F7 75 46 09 CF 4F 3C- AES 연산 과정
- Key Expansion (키 확장): 여러 개의 라운드 키 생성
- AddRoundKey (키 추가): 평문과 키를 XOR 연산
- SubBytes (바이트 치환): S-Box를 이용해 바이트 단위 치환
- ShiftRows (행 이동): 바이트들을 왼쪽으로 회전
- MixColumns (열 섞기): 수학적 변환으로 데이터를 섞음
- AddRoundKey (키 추가): 다시 XOR 연산 수행
- 암호문 (Ciphertext)
3A D7 7B B4 0D 7A 36 60
A8 9E CA F3 24 66 EF 97- 복호화
- 위 과정을 역순으로 수행하면 원래 평문으로 복원된다.
복잡한 과정이 들어가는데 간단하게 요약하면 평문을 잘라서 키랑 혼합하여 암호문을 만드는 과정이다. 자르다보니 자른 블럭과 키가 크기가 안 맞을 경우에 대비해 여러가지 방식을 추가한 것 뿐이다.
RSA
rsa는 공개키와 개인키를 사용해 데이터를 암호화/복호화를 한다. 공개키는 평문을 암호화할 때 키로 사용하고 개인키는 암호문을 복호화할 때 사용한다. 생각해보면 암호화하는 것은 모두에게 공개해도 되지만 복호화하는 것은 특별한 사람만 평문을 봐야하기 때문에 개인키라고 생각하면 된다.
공개키와 개인키는 한번에 생성하는데 아래와 같은 방식으로 생성한다.

위 내용에서 중요한 점은 공개키를 만들 때 소수 2개를 선택하고 그 값을 통해 개인키도 계산하는데 이 과정을 공개키를 알고 있는 상태에서 개인키를 유추하는 것이 현대 컴퓨터로는 많은 시간이 걸리기 때문에 유추할 수 없다는 점이다. 그래서 위 수식을 통해 만든 과정을 통해 공개키로 암호화 했지만 공개키로 복호화하지 못하고 개인키로는 복호화 가능한 특징과 개인키를 공개키로를 통해 유추하는 연산이 너무 오래 걸려 유추하기 힘든 특징을 가지고 RSA를 통해 암호화/복호화를 진행한다.
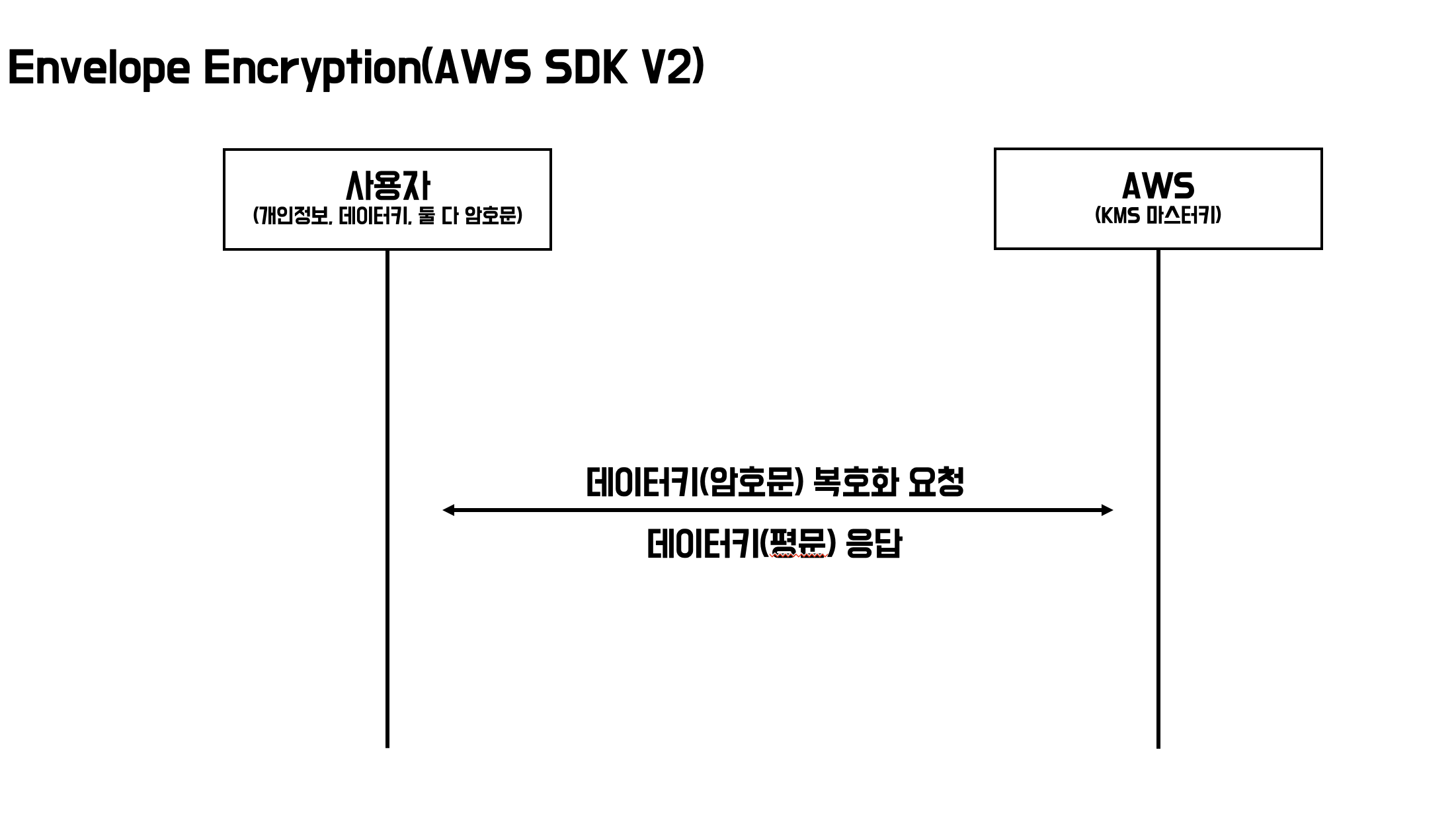
봉투 암호화
고전 암호학에서는 암호화를 하기 위해 알고리즘 하나를 사용했더니 어떤 알고리즘을 사용했는지 알면 암호문을 통해 평문을 쉽게 구할 수 있었다. 그리고 키를 추가하여 혼합하여 암호화 했더니 마찬가지로 키 값과 알고리즘만 안다면 암호문을 통해 평문을 다시 쉽게 알 수 있는 단점이 있다. 그래서 키 자체도 보안적인 장치로 잘 보관해야 한다는 이슈가 발생한다.
AWS 같은 이런 것을 해결하기 위해 KMS Service를 제공해준다. KMS Service는 암호화할 대상(개인정보 등) 뿐만 아니라 키 값도 암호화해준다. SDK v2부터는 내부적으로 키 값을 알아서 암호화하고 암호화할 데이터만 전달해주면 알아서 복호화해서 전달도 해준다.

'etc' 카테고리의 다른 글
| 자동 완성 기능 구현하기(with 엘라스틱 서치) 2편 (0) | 2024.08.09 |
|---|---|
| 자동 완성 기능 구현하기(with 엘라스틱 서치) 1편 (4) | 2024.08.08 |
| FEP 통신 내재화(with Spring Integration TCP) (0) | 2024.07.03 |
| VectorDB에 대하여 (0) | 2024.06.19 |
| 손해보험에 대해서 (0) | 2023.01.03 |

